おもしろ科学実験室（工学のふしぎな世界）
レーザーポインターで測るCDの溝間隔
三重大学 工学部
図1 CD（DVD）上のデーターの様子普段使っているCDやDVD。直径12㎝の小さなディスクに音楽や映画が詰まっています。どうやってこの中にそんなに大量な情報を入れているのでしょうか？不思議です。実はこれらのメディアには、小さな凹凸が円周状のトラックに並んでおり、この凹凸を使って音楽等の情報を記録しているのです（図１）。とういわけで、ここでは、普段プレゼンテーションで使っているレーザーポインター光の回折現象を使って、CDやDVDのトラック方向の溝間隔を測ります。
用意するもの
写真１ 実験道具- 写真1に示したCDやDVD
- 市販のレーザーポインター（何色でもOK。波長をλとします）
- 定規や巻尺
- シャープペン
- 大きめ（A3）のコピー用紙や方眼紙
- 必要ならば、サングラス等の保護メガネ
- 細かめの網（布でも可）等
CDやDVDは人に持ってもらっても良いですし、固定台にワニ口クリップ等で取り付けても良いです。大きめ紙は、中央に穴を開けて、何かに吊り下げるか、立てかけておきます。紙は人に持ってもらっても良いです。
実験方法
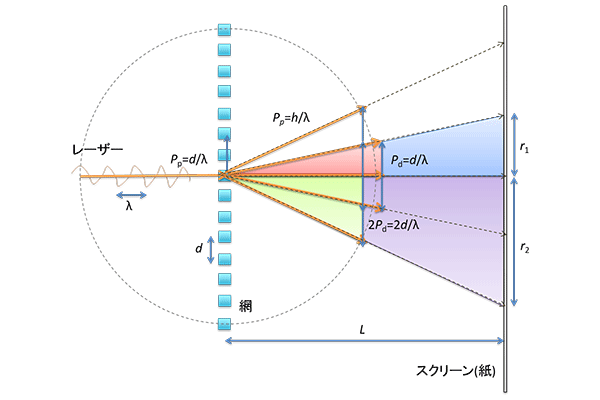図２ 網を使った透過型の回折実験の概略図まず、網の目の間隔を目視で測ります。図２のように網と紙(スクリーン)とレーザーを設置します。今回は、細かめの金網で、虫眼鏡を使ってみたところ、21本の網の間隔が5mmでした。よって網一つの間隔（dm）は0.25mmとなります。網は粗いものでも構いませんが、その場合はLの距離を長く取ってください。
写真2 網の回折パターン次にこの網にレーザーを照射して、網上の照射点からL（今回は3000mm）離れた地点にコピー用紙を置きます。すると網をかざす前は1点だった紙上の照射点が複数の回折点に分かれます（写真２）。今回は中央から左右斜めの４つ目の回折点までの距離（r4）を測ったところ、いずれも30mmでした。図２に示す運動量の変化から（詳細は後に述べます）、以下の式が成り立ちます。ここでhはプランク定数（6.6×10-34Js）ですが、比を取るので関係ありません。
p4:pp=4h/dm : h/λ=4λ:dm= r4: (L2+ r42)1/2
よって、各測定値を代入すると
4λ:dm= 30mm:((3000mm)2+ (30mm)2)1/2=30:3000.15
となり、レーザー光の波長（λ）=0.00063mm=0.63μm=630nmと求まります。
図3 CDを使った反射型の回折実験の概略図次に中央の穴にレーザーを通過させて、反対側に紙から距離L’（今回は100mm）離したCDに照射させます（図３）。CDで反射した光は、紙に写真３のような回折点になって現れます（写真では中央の照射点（０次回折点）が穴の部分にあり見えていません）。0次回折点の次に見える二つの点が１次回折点で、今回は左が44mm、右が45mmでした（よって平均r1=44.5mm）。
写真３ CDの回折パターンさらに離れてその外側に見える二つの点が２次回折点で、今回は左が143mm、右が127mmでした（よって平均r2=135mm）。中央の０次回折点が分からないときは、左右の同じ回折点の距離を測って２で割ってください。他方、写真にはこれとは別の方向に別の１次回折点が見えます（r’1=28mm）。CDのトラックの間隔をdr、円周方向の穴の平均間隔をdcとします。照射された光はトラック方向に前者の回折点（r1=44.5mm、r2=135mm）が、円周方向に後者の回折点（r’1=28mm）が現れます。
まずトラック方向の回折点について、網のときと同じ原理で計算します。
（１次回折点の場合）
p1:pp=h/dr : h/λ=λ: dr= r1:(L’2+ r12)1/2
よって、各測定値を代入すると
λ:dr=630nm: dr =44.5mm:((100mm)2+ (44.5mm)2)1/2=44.5:109.5
となり、トラックの間隔は、dr=1550nm=1.6μmと求まります。
（２次回折点の場合）
p2:pp=2h/dr : h/λ=2λ: dr= r2:(L’2+ r22)1/2
よって、各測定値を代入すると
2λ:dr=1260nm:dr = 135mm:((100mm)2+ (135mm)2)1/2=135:168
となり、トラックの間隔は、dr=1570nm=1.6μmと求まります。この値は１次回折で求めたものに近く、両者ともにおおよその値が一致することが分かります。CDのトラックの間隔がdr=1.6μmであることは、CDの規格表とも一致し、正しいことが分かります。ちなみに円周方向の回折点についても、同じ原理で計算します。
（１次回折点の場合）
p1:pp=h/dc : h/λ=λ: dc= r’1:(L’2+ r’12)1/2
よって、各測定値を代入すると
λ:dc=630nm: dc = 28mm:((100mm)2+ (28mm)2)1/2=28:103.8
となり、円周方向のデーターの間隔は、dr=2340nm=2.3μmと求まります。円周方向には様々なデーターが並んでおり、一般に周期性はありません。ところがこの事実は、データーがこの間隔ごとにグループを作って書き込まれていることを示しています。
写真４ DVDの回折パターン次に同じ条件でDVDに照射させます。反射した光は、紙に写真４のような回折点になって現れ、 0次回折点とトラック方向の１次回折点の距離は、左が181mm、右が166mmでした（よって平均r1=173.5mm）。0次回折点と円周方向の１次回折点の距離は、r’1=22mmでした。
トラック方向の回折点について、CDのときと同じ原理で計算すると、
p1:pp=h/dr : h/λ=λ: dr= r1: (L’2+ r12) 1/2
λ:dr=630nm: dr = 173.5mm:((100mm)2+ (173.5mm)2)1/2=173.5:200.3
となり、トラックの間隔dr=720nm=0.72μmと求まります。DVDのトラックの間隔がdr=0.72μmであることは、DVDの規格表とも一致します。
一方、円周方向の回折点については、１次の回折点が出ているものと考えて、同じ原理で計算すると、
p1:pp=h/dc : h/λ=λ: dc= r’1:(L’2+ r’12)1/2
λ:dc=630nm: dc = 22mm:((100mm)2+ (22mm)2)1/2=22:102.4
となり、円周方向のデーターの間隔はdr=2930nm=2.9μmと求まります。DVDも円周方向に一定間隔で書き込みがなされているようです。
原理
よく調べてみるとCDやDVDを使った回折実験は、よく取り上げられているようです。そこで以下では、従来と異なり、光と格子の運動量からこの現象を説明してみたいとおもいます。高校物理Ⅱの教科書をみると、最後の方にド・ブロイの式が載っています。粒子性の象徴である運動量pと波動性の象徴である波長λの関係を表す式です。
p =h/λ
ここで、hはプランク定数（6.6×10-34Js）です。
つまり、レーザーポインターから出る同じ波長の光は、小さな光の粒（光子）の集まりで、一つ一つは同じ大きさの運動量を持つ粒子となります。今回の場合、波長λ=630nmの光の運動量ppは、以下のように表されます。
pp= h/λ=6.6×10-34Js/6.3×10-7m=1.05×10-27 Ns
周期的な波長を持つ光が運動量を持つように、幅dの周期的な回折格子からなるCDやDVDも、dを波長と同じと見なせば、pd=h/dの運動量を持つことになります（反対側に同じ運動量を持つことで現れる仮想運動量なのですが。。。）
光の粒がCDやDVDを通りすぎる際に、回折格子からの粒子と衝突すれば、運動量の方向が変化しますが、エネルギーは変化しないので、運動量自体の大きさは変化しません。よって図２や図３に示すような運動量の関係式が成り立ちます。
１次回折の場合、光子は１個の格子の運動量とぶつかります。よって、直角三角形の斜面の長さはpp=h/λ、垂直方向の一辺の長さはpd =h/dとなります。
一方、２次回折の場合、光子は２個の格子の運動量とぶつかります。よって、直角三角形の斜面の長さはpp=h/λ、垂直方向の一辺の長さは2 pd =2h/dとなります。そういえば、網では沢山の回折点が観察されたのに、CDやDVDでは１次か、２次の回折点しか観察されませんでした。これはなぜだか分かりますか？
図２や図３から説明がつくと思いますので考えてみてください。
参考文献
- 若林文高、Bull. Natn. Sci. Mus., Tokyo, Ser. E, 28, pp. 21-30 (2005)
http://www.kahaku.go.jp/research/publication/sci_engineer/download/28/BNSM_E2803.pdf - 若林文高、濱田浄人、現代化学、2005年4月号、p.50-53 (2005)
- 若林文高、現代化学、1990年4月号、p.23-25 (1990)
| 掲載大学 学部 |
三重大学 工学部 | 三重大学 工学部のページへ>> |
関連記事
三重大学
工学部
- 総合工学科 総合工学コース
- 総合工学科 機械工学コース
- 総合工学科 電気電子工学コース
- 総合工学科 応用化学コース
- 総合工学科 建築学コース
- 総合工学科 情報工学コース
