おもしろ科学実験室(工学のふしぎな世界)
状態フィードバック制御を用いて振子を立たせよう
東京海洋大学 海洋工学部
准教授 小池雅和
はじめに
図1のように、手のひらで傘や棒を立たせるといった遊びを子供の頃、挑戦したことはありませんか?この遊びを題材にした実験をしてみたいと思います。この遊びを模擬したもので「倒立振子」と呼ばれる装置があります。この装置は制御工学の分野では不安定なシステムとして知られており、制御の勉強をするための題材として良く用いられています。倒立振子にも幾つか種類がありますが、ここでは図2の「回転型倒立振子」(「古田ペンデュラム」とも呼ばれる)を用いたいと思います。ここでは、振子の倒立状態を維持させるような入力パターンを探してみたいと思います。
 図1:手のひらで棒を立てる
図1:手のひらで棒を立てる 図2:回転型倒立振子
図2:回転型倒立振子準備するもの
- 回転型倒立振子(市販のキットも販売されています。)
人が棒を手のひらで立たせるプロセス
この装置の説明の前に、まずは、人が棒を手のひらに立たせる時どうようなプロセスを経ているのかを考えてみましょう。棒が倒れそうになったら、倒れた方向に手のひらを動かすことで倒立状態を維持させるのがコツですよね?このとき、人は図3(ブロック線図)のような流れで信号を処理しています。制御対象からの信号が棒の角度になります。この信号が信号y1です。まず、目で棒の角度を認識するわけですね。この信号が信号y2です。 一方、我々は目標状態である「棒の倒立状態」を思い描いているわけです。この信号が信号rです。 そして、目標値と棒の角度の差分である信号e、すなわちどのくらい倒れたか?を認識するわけです。この差分信号eが脳に入り、どのくらい手のひらを動かせば良いか判断し、制御対象に「手のひらの移動量」である信号uを入力するわけです。このループを短い周期で何度も回していることになります。
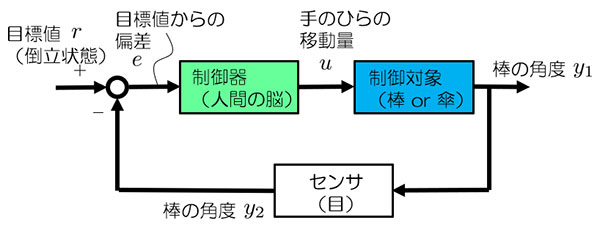 図3:信号の流れ
図3:信号の流れ人は図1のような短い棒(ペン)では倒立状態を維持させることができません。その理由は短い棒は素早く倒れてしまうのですが、人の処理能力では追い付かないからです。しかし、図3の信号処理を機械で素早く実行させることで、短い棒でも倒立状態を維持させることが可能です。これを実現した装置が回転型倒立振子です。
装置構成
では話をもとに戻し、装置構成の説明をしましょう。この装置は主に、図4のように振子、アーム、サーボモータ、エンコーダ、DSP(デジタルシグナルプロセッサ)から構成されております。振子が棒(ペン)で、回転アームが手のひらに相当します。動画1をご覧ください。振子はベアリングを介してアームに接続しているので、ほとんど摩擦はなく、回転フリーな状態です。またアームはサーボモータに直結しており、サーボモータに電圧を入力すると、回転します(動画1の後半)。ちなみに電気回路図は図5のようになります。
 図4:装置構成
図4:装置構成動画1:動作確認
 図5:電気回路図
図5:電気回路図今回の装置では、アームの角度はアームに直結しているサーボモータについているエンコーダで検出できます。また、振子の角度も別途エンコーダで検出しています。それぞれの角速度は計測していませんが、差分演算で推測することが可能です。よって、振子の角度 、振子の角速度
、振子の角速度 、アームの角度
、アームの角度 、アームの角速度
、アームの角速度 の四つの信号をモニタリングすることができます。倒立状態を維持させるためには、この四つの信号の状態に依存してサーボモータへの指令トルク
の四つの信号をモニタリングすることができます。倒立状態を維持させるためには、この四つの信号の状態に依存してサーボモータへの指令トルク を適宜変化させる必要があります。今回用いる指令トルク
を適宜変化させる必要があります。今回用いる指令トルク を式で書くと、
を式で書くと、

となります。これは「状態フィードバック入力」と呼ばれています。今回の実験では、この から
から の値を変えて挙動を確認したいと思います。なお、
の値を変えて挙動を確認したいと思います。なお、 から
から を「ゲイン」と呼びます。
を「ゲイン」と呼びます。
入力パターンによる挙動
以下の二つのパターンのゲインで挙動を確認しましょう。
パターン1

パターン2

以下の動画をごらんください。
動画2:パターン1のゲインを用いた場合
動画3:パターン2のゲインを用いた場合
パターン1、パターン2ともに倒立状態を維持することができます。多少の外乱を加えても維持し続けることが可能です。また、パターン2では、アームを回転させながら倒立状態を維持させるような挙動になっています。ゲインの値を少し変えるだけで、全く異なる動きを持たせることができるのです。ちなみに、振子が下側に垂れ下がった状態から倒立させることも可能です。この挙動が動画4になります。
動画4:振り上げ制御
解説
闇雲にゲインの値を選んでも倒立状態を維持させることはできません。ここでは、倒立状態を維持できるような適切なゲインの探し方を大雑把に解説します。システムを意のままに操るためには、システムの本質を知る必要があります。今回の回転型倒立振子の場合で言えば動きを支配する運動方程式を知る必要があります。詳細は省略しますが、以下の二本の式が回転型倒立振子の運動方程式になります。文字の定義は図6を参照ください。


 図6:文字の定義
図6:文字の定義さらに、振子の質量や慣性モーメントなどの値を正確に測定しておく必要があります。上記の運動方程式は非線形方程式ですが、これを線形近似してまとめると、一階の連立微分方程式の形に落とし込むことができます。制御工学の分野ではこれを「状態方程式」と呼んでいます。式で書くと以下のようになります。

ここで、 と
と はベクトル、
はベクトル、 はスカラ、
はスカラ、 は行列となります。システムの特徴は
は行列となります。システムの特徴は と
と に凝縮されたことになります。まずは、入力が無い場合、すなわち、
に凝縮されたことになります。まずは、入力が無い場合、すなわち、 の場合を考えてみましょう。これはサーボモータに電圧を加えない場合に相当しています。システムの特徴は
の場合を考えてみましょう。これはサーボモータに電圧を加えない場合に相当しています。システムの特徴は のみに凝縮されていることになります。そして、不安定なシステムか否かはこの行列
のみに凝縮されていることになります。そして、不安定なシステムか否かはこの行列 の固有値を調べることで判別できることが知られています。興味のある方は固有値について自分で調べてみてください。固有値の実部が負になれば安定なシステムです。次に入力がある場合、すなわち、
の固有値を調べることで判別できることが知られています。興味のある方は固有値について自分で調べてみてください。固有値の実部が負になれば安定なシステムです。次に入力がある場合、すなわち、 の場合を考えましょう。
の場合を考えましょう。 はベクトルで、先に登場したゲイン
はベクトルで、先に登場したゲイン から
から に相当します。
に相当します。 を状態方程式に代入すると、
を状態方程式に代入すると、

を得ます。これは、入力を施した後のシステムの状態方程式になります。行列 がシステムの安定性を決めていることに気づくと思います。行列
がシステムの安定性を決めていることに気づくと思います。行列 の固有値の実部が負になるようにゲイン
の固有値の実部が負になるようにゲイン を選んでおけば、システムは安定化できるわけです。先に挙げたパターン1のゲインは上記のように選んでいます。
を選んでおけば、システムは安定化できるわけです。先に挙げたパターン1のゲインは上記のように選んでいます。
最後に
状態フィードバック制御は様々な場面で用いられています。この実験をきっかけにして制御工学に興味をもって頂けたら幸いです。
| 掲載大学 学部 |
東京海洋大学 海洋工学部 | 東京海洋大学 海洋工学部のページへ>> |