おもしろ科学実験室(工学のふしぎな世界)
タイリングの数理と芸術的タイリングの作成
徳島大学 理工学部 情報光システムコース
永田 裕一
はじめに
日常何気なく目にするものの中にもその背後に数学的な構造が潜んでいることは多く、そういった構造を意識するかしないかで物の見え方も変わってくるものです。今回はタイリングの背後に潜む数学的な構造の一端を紹介し、これを利用してエッシャータイリングと呼ばれる芸術的タイリングの作成を行う。
タイリングとは有限種類の図形で平面を隙間なく敷き詰めたものである。最も典型的なタイリングとしては正方形やレンガのような長方形で構成されるものが思い浮かぶであろう。オランダの芸術家M.C.Escher (1898-1972)は図1のような芸術的なタイリングを数多く創出したことで有名である。この例のように、動物のような意味のある図形1つを敷き詰めて構成するタイリングはエッシャータイリングと呼ばれている。芸術的なエッシャータイリングを作成することが難しいことは容易に想像できるであろう。
それでは、エッシャータイリングをデザインしていきましょう。
 図1:エッシャータイリングの例。
図1:エッシャータイリングの例。準備するもの
- 紙、鉛筆、消しゴム
- 定規、コンパス(必要であれば)
- 適当なお絵描きソフトとそれを動かすPCがあると良い(必須ではない)。
原理
図2に平面を1種類のタイル図形で敷き詰めた例を示している。この例では4つの網掛けした部分の形状を1つの単位として、それを平行移動して並べることで平面全体を敷き詰めていることが分かる。このようなタイリングのクラスをIsohedral Tilingと呼ぶ。図1もIsohedral Tilingの一例である。Isohedral Tilingはタイル図形の隣接の仕方に基づいて93種類のタイプに分類できることが知られており、IH1、IH2、…、IH93と名前が付けられている。
各IHタイプに属する任意のタイル図形は、そのIHタイプの特徴を表現するテンプレートを変形することで得ることができる。例えば、図3(a)にIH51のテンプレートを示している。このテンプレートは四角形であるが、対となるJ枝と2本のS枝で構成される。対となるJ枝は同じ形であれば自由に変形することができる。ただし、2つのJ枝は赤い矢印が重なる向きで重ね合わせた時に同じ形である必要がある。個々のS枝は枝の中心に対して点対称であるという条件の下で自由に変形できる。ただし、このようにテンプレートを変形して得られたタイル図形に自己交差があってはならない。図3(b)にこのテンプレートを変形して得られたタイル形状の例を示している。ここで、テンプレートの辺の変形だけでなく、頂点も移動していることに注意すること。これは図2に示したタイリングを構成するタイル図形となっている。
テンプレートに従ってタイル図形を生成したら、この図形を並べることで必ずタイリングすることができる。タイル図形をどのように並べれば良いかは図4を見ると分かる。この図はIH51のテンプレートの隣接関係を示しており、このテンプレートに対応するタイル図形をコピーしたものを平行移動して敷き詰めることで平面全体を覆うことができる。
Isohedral Tilingについてもっと詳しく知りたい人は、下記のサイト(英語)の情報が参考になる。
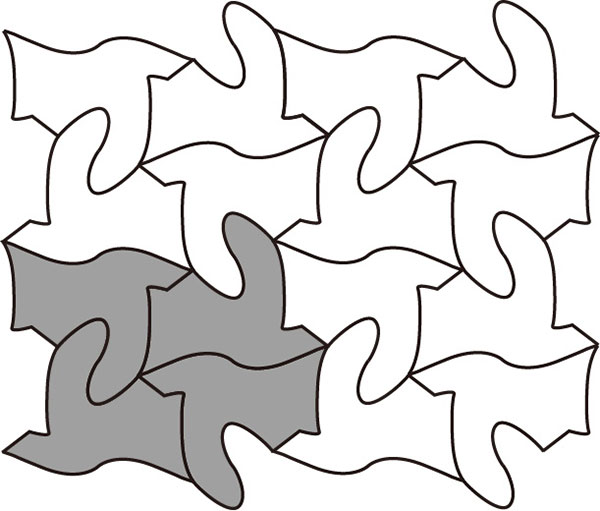 図2:Isohedral Tiling (IH51)の例。
図2:Isohedral Tiling (IH51)の例。 図3:(a)IH51のテンプレートと(b)テンプレートから得られるタイル図形の例。
図3:(a)IH51のテンプレートと(b)テンプレートから得られるタイル図形の例。 図4:IH51のテンプレートの隣接関係。
図4:IH51のテンプレートの隣接関係。作り方
93種類のIHタイプの中で、最も柔軟に変形できるタイプがIH4である。IH4のテンプレートを図5に示しているので、これを変形してタイル形状を設計すると良い。どのような手順が良いかは一概に言えないが、例えば次の順序でテンプレートの条件を満たすタイル形状およびタイリングを生成することができる(図6参照)。
- 平行で長さが等しい直線を引く(これが対となるJ枝になる)。
- 先の線分上に無い2点の位置を決め、2つの線分と選んだ2点をつないで6角形を作る。新たに生成された4つの辺がS枝となる。
- 生成した6角形がIH4のテンプレートとなり、テンプレートの各辺を制約に従って変形する。
- 気に入ったタイル形状が完成したら、タイリングの隣接関係に従ってタイリングを完成させる。
コメント
- ステップ1、2、3を試行錯誤することで、好みのタイル図形を設計する。この段階では厳密にテンプレートの制約を満たすように図形を描かず、フリーハンドで大まかに設計するのが良いだろう。
- ステップ1、2、3で大体のタイル図形が決定したら、テンプレートの制約を満たすように正確にタイル図形を描く。
- ステップ1から4は全て手書きで行うこともできるが、適当なお絵描きソフトを併用すると作業効率が良いだろう(特にステップ4)。
- タイル図形の内部に絵を描くことで、タイリングの芸術性が向上する。
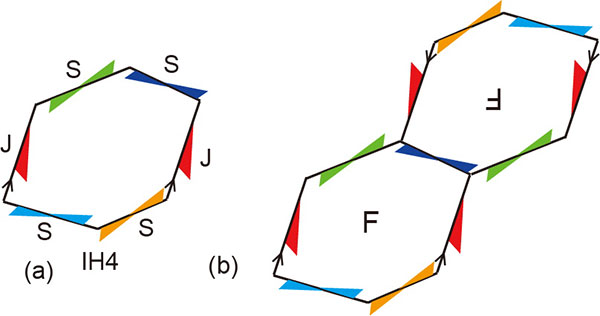 図5:(a)IH4のテンプレート。対となるJ枝は互いに平行。S枝の長さや向きに制限はない。(b) IH4のテンプレートの隣接関係。
図5:(a)IH4のテンプレート。対となるJ枝は互いに平行。S枝の長さや向きに制限はない。(b) IH4のテンプレートの隣接関係。 図6:タイリングの生成手順.生成したタイル図形はカメのつもり。
図6:タイリングの生成手順.生成したタイル図形はカメのつもり。| 掲載大学 学部 |
徳島大学 理工学部 | 徳島大学 理工学部のページへ>> |